数值最优化方法 英文

先用Python画出等高线图和3D图看一下函数的样子，极小点应该大致位于下图五角星的位置。

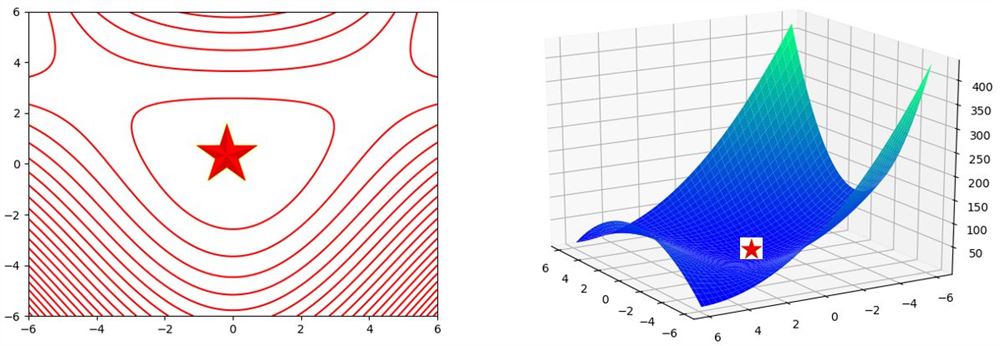
下面使用基本Newton法和LM算法来求解该问题。

算法1.基本Newton方法基本Newton方法指取全步长 的Newton方法。

基本Newton方法的迭代步骤：

1.给出 , ,

2.若终止准则满足，则输出有关信息，停止迭代

3.由方程组 计算 ，式中 和 分别为 在第k次迭代时二阶导数和一阶导数的值。（注：此时需满足 正定，划重点！！！）

4. , ,转步2

Python代码实现如下，实现时进行了可视化来显示每次迭代过程，并可以输出第k次的迭代点坐标值以及函数值。

from sympy import *import numpy as npimport mathfrom matplotlib import pyplot as pltdef get_Hessian(data): dx1x1 = y.diff(x1,x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx1x2 = y.diff(x1,x2).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2x1 = y.diff(x2,x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2x2 = y.diff(x2,x2).subs(x1,data[0]).subs(x2,data[1]).evalf() return np.array([[dx1x1, dx1x2],[dx2x1, dx2x2]])def get_Jacobian(data): dx1 = y.diff(x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2 = y.diff(x2).subs(x1,data[0]).subs(x2,data[1]).evalf() return np.array([[dx1],[dx2]]), math.sqrt(dx1**2+dx2**2)def plot_contour(): x = np.linspace(-6,6,100) y = np.linspace(-6,6,100) X,Y = np.meshgrid(x,y) Z = 3*X**2+3*Y**2-X**2*Y plt.contour(X, Y, Z, 25, colors = 'red', linewidth = 0.5)if __name__ == "__main__": # 打开交互模式 plt.ion() # 绘制等高线 plot_contour() plt.xlabel('x1') plt.ylabel('x2') # 定义迭代过程需求解的函数 x1,x2,y = symbols("x1 x2 y") y = 3*x1**2+3*x2**2-x1**2*x2 # 定义起始点 x_initial = [1.5,1.5] x_k=x_initial xx = [] yy = [] zz = [] xx.append(round(x_k[0],4)) yy.append(round(x_k[1],4)) zz.append(round(y.subs(x1,x_k[0]).subs(x2,x_k[1]).evalf(),4)) print("({:.4f},{:.4f}), {:.4f}".format(xx[0], yy[0], zz[0])) plt.plot(xx,yy,c='black') plt.scatter(xx,yy,s=30,c='b') plt.pause(5) for i in range(1,7): Gk = get_Hessian(x_k) Gk = Gk.astype(float) gk, gknorm = get_Jacobian(x_k) gk = gk.astype(float) Gk_inverse = np.linalg.inv(Gk) dk = np.dot(Gk_inverse, gk) dk = dk.T[0] x_k = [x_k[0]-dk[0],x_k[1]-dk[1]] xx.append(round(x_k[0],4)) yy.append(round(x_k[1],4)) zz.append(round(y.subs(x1,x_k[0]).subs(x2,x_k[1]).evalf(),4)) print("({:.4f},{:.4f}), {:.4f}".format(xx[i], yy[i], zz[i])) plt.plot(xx,yy,c='black') plt.scatter(xx,yy,s=30,c='b') plt.pause(5) if gknorm = 10e-6: break plt.ioff() plt.show()

对于起始点为 ，迭代过程如下，经过千辛万苦最终还是到达了五角星的附近。

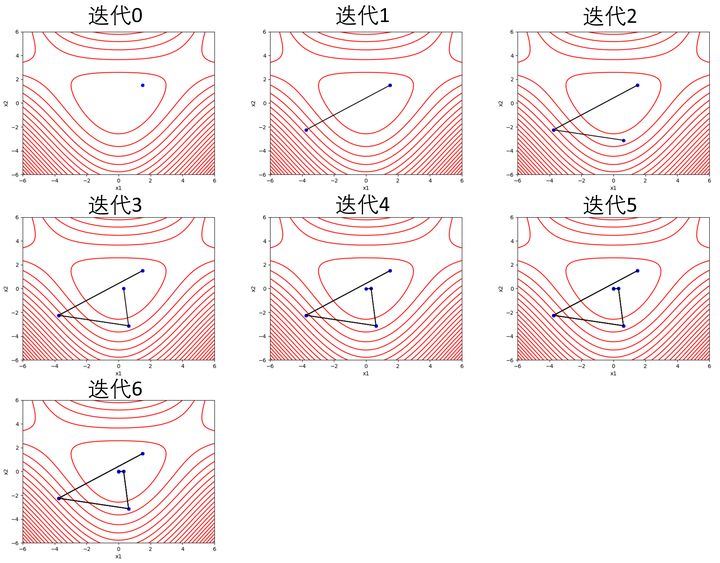图中，红色线为等高线迭代点及其函数值

起始点为 ，其最终迭代结果如下，这次并没有太幸运，没有胜利到达五角星。

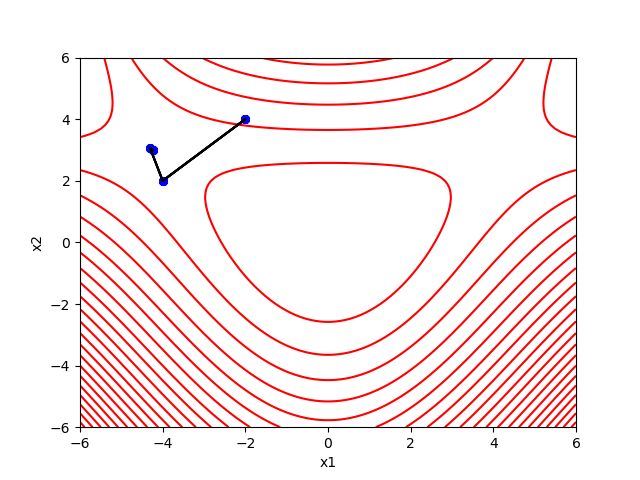
起始点为 时，由于此时 为奇异阵，此时基本Newton法失败。干脆就直接罢工了。由此可见，基础Newton法求最优化问题对于初始点的选择要求较高，初始点选取的不好，算法结果会较差。

在迭代过程中出现G非正定的情况亦会导致Newton法失败。算法2的LM方法可以解决该问题。

算法2.LM方法

LM方法即Levenberg-Marquardt方法，是处理 奇异、不正定等情形的一个最简单且有效的方法。该方法将基本Newton法第3步求解步长的方程 更改为

式中 , 为单位阵。当 也不正定时，简单令 即可。

Python实现如下：

from sympy import *import numpy as npimport mathfrom matplotlib import pyplot as pltdef get_Hessian(data): dx1x1 = y.diff(x1,x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx1x2 = y.diff(x1,x2).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2x1 = y.diff(x2,x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2x2 = y.diff(x2,x2).subs(x1,data[0]).subs(x2,data[1]).evalf() return np.array([[dx1x1, dx1x2],[dx2x1, dx2x2]])def get_Jacobian(data): dx1 = y.diff(x1).subs(x1,data[0]).subs(x2,data[1]).evalf() dx2 = y.diff(x2).subs(x1,data[0]).subs(x2,data[1]).evalf() return np.array([[dx1],[dx2]]), math.sqrt(dx1**2+dx2**2)def plot_contour(): x = np.linspace(-6,6,100) y = np.linspace(-6,6,100) X,Y = np.meshgrid(x,y) Z = 3*X**2+3*Y**2-X**2*Y plt.contour(X, Y, Z, 25, colors = 'red', linewidth = 0.5)def judge_positive(G_k): # 计算特征值，当特征值均大于0时矩阵正定 eigenvalue,featurevector=np.linalg.eig(G_k) for i in eigenvalue: if i = 0: return False return Trueif __name__ == "__main__": # 打开交互模式 plt.ion() # 绘制等高线 plot_contour() plt.xlabel('x1') plt.ylabel('x2') # 定义迭代过程需求解的函数 x1,x2,y = symbols("x1 x2 y") y = 3*x1**2+3*x2**2-x1**2*x2 # 定义起始点 x_initial = [-2,4] x_k=x_initial # 定义vk vk = 3.02 xx = [] yy = [] zz = [] xx.append(round(x_k[0],4)) yy.append(round(x_k[1],4)) zz.append(round(y.subs(x1,x_k[0]).subs(x2,x_k[1]).evalf(),4)) print("({:.4f},{:.4f}), {:.4f}".format(xx[0], yy[0], zz[0])) plt.plot(xx,yy,c='black') plt.scatter(xx,yy,s=30,c='b') plt.pause(1) for i in range(1,7): Gk = get_Hessian(x_k) Gk = Gk.astype(float) I = np.identity(2) Gk_plus = Gk + vk*I # 判断Gk + vk*I的正定性 if judge_positive(Gk_plus): Gk = Gk_plus else: Gk = Gk + 2*vk*I gk, gknorm = get_Jacobian(x_k) gk = gk.astype(float) Gk_inverse = np.linalg.inv(Gk) dk = np.dot(Gk_inverse, gk) dk = dk.T[0] x_k = [x_k[0]-dk[0],x_k[1]-dk[1]] xx.append(round(x_k[0],4)) yy.append(round(x_k[1],4)) zz.append(round(y.subs(x1,x_k[0]).subs(x2,x_k[1]).evalf(),4)) print("({:.4f},{:.4f}), {:.4f}".format(xx[i], yy[i], zz[i])) plt.plot(xx,yy,c='black') plt.scatter(xx,yy,s=30,c='b') plt.pause(1) if gknorm = 10e-6: